10792. История Лорела - Харди

 

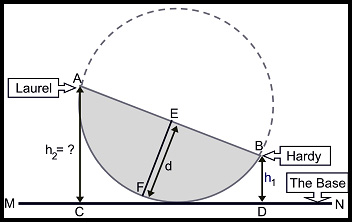
Пила по дереву имеет вид сегмента AFB окружности радиуса r. Харди садится на конец B, а Лорел – на конец A (Харди тяжелее Лорела). Известно расстояние d = FE между серединой отрезка AB и серединой дуги AFB. Расстояние от точки B до земли равно h1. Найти h2 – расстояние от точки A до земли.

 

\epsfbox{p10792b.eps}

 

Вход. Первая строка содержит количество тестов n (0 < n £ 1000). Каждый тест содержит три числа r, d и h1 (10 £ r £ 100, 5 £ d £ r, 5 £ h1 £  d).

 

Выход. Для каждого теста вывести в отдельной строке его номер и величину h2, округленную до четырех десятичных знаков.

 

Пример входа

2
10 10 10
10 7 6

 

Пример выхода

Case 1: 10.0000
Case 2: 8.0342

 

 

РЕШЕНИЕ

геометрия

 

Анализ алгоритма

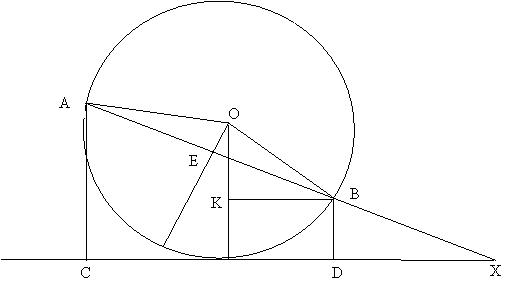
В треугольнике OEB: OB = r, OE = r – d, sin ÐEBO = (r – d) / r. В треугольнике OKB: OB = r, OK = r – h1, sin ÐKBO = (r – h1) / r. Находим ÐKBA = ÐKBO – ÐEBO.  Из треугольника OEB: EB = , AB = 2 * EB. Из треугольника BDX: BX = BD / sin ÐDXB = h1 / sin  ÐKBA. Находим AX = AB + BX. Из треугольника ACX находим ответ: h2 = AC = AX * sin ÐDXB.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 


Реализация алгоритма

Вычисляем b = ÐKBA = ÐKBO – ÐEBO = arcsin(r – h1) / r – arcsin(r – d) / r. Если b = 0, то точки A и B находятся на одинаковом расстоянии от земли (прямой CX) и h2 = h1. Иначе вычисляем AX = 2 *  + h1 / sin ÐKBA и находим ответ h2 = AX * sin ÐDXB (ÐDXB = ÐKBA).

 

scanf("%d",&t);

for(i = 0; i < t; i++)

{

  scanf("%lf %lf %lf",&r,&d, &h1);

  printf("Case %d: ",i+1);

  b = asin((r - h1)/r) - asin((r-d)/r);

  if (b == 0.0)

  {

    printf("%0.4lf\n",h1);

    continue;

  }

  ax = 2 * sqrtl(r*r - (d-r)*(d-r)) + h1/sin(b);

  h2 = ax * sin(b);

  printf("%0.4lf\n",h2);

}